Proof Of Afterlife By Geometry
Theorem: Pyramid Analogy: Consciousness (a point of view) can be likened to the apex. Memory (surrounding space) can be likened to the base or environment. This visualizes the mathematical relationship between memory and consciousness awareness.
Afterlife Geometry Theorem
1. Geometry: The Math that Proves Afterlife
1.1. Basic Geometric Elements: Point, Line, Plane, and Space
When it comes to afterlife, the realm of mathematical truth has thus far remained veiled and no scholar has unveiled a rigorous proof of the afterlife's existence. The enigma is that an afterlife proof is beyond human understanding. Thus, while wondrous tales abound, the enigmatic afterlife proof is elusive in the field of human understanding.
The realm of afterlife has remained beyond the reach of mathematical proofs, until now. This is a mathematical theory that shall unveil the very essence of the afterlife. Geometry may seem like a strange vehicle for such a revelation, but I ask you to set aside skepticism and journey with me through these thought experiments.
We commence with a brief introduction to geometry - the field of mathematics that explores the wonders of space and time. In this realm of shapes and dimensions, we shall find the essence of our pursuit. Geometry has a bearing on afterlife. Consider that in the realm of three-dimensional software, complete environments are created entirely from geometry. Models made from geometry are as realistic and detailed as the world that surrounds us now. Three-dimensional modeling holds its environment in memory, yet it is stored as geometric formulas. As one looks at three-dimensional, computer-generated worlds, it is apparent that we are getting very close to reality itself. It is plausible that proof of afterlife could be based on geometry.
We start with a review of the basic elements of geometry - point, line, plane, and space. Then we build our thought experiments based on these elemental concepts.
1.2. Basic Geometric Element One: The Point
A point signifies a precise location, such as the position of a camera in three-dimensional software like Blender. Unlike an object, a point has no dimension; it's akin to a tiny dot in your mind's eye, infinitely small, without length, width, or height. Visualize it as a pinpoint of light in a vast expanse of darkness - a pure position in space. It looks like this:

This is an artists rendition of a geometric point. Geometrically the point has no dimension. This is referred to as 0D, meanin it has no length, width, depth, or duration. Here it is envisioned as a pont of light, shining against a black background.
1.3. Basic Geometric Element Two: The Line
A line is thin. A line is so thin that it has no height or width. However, it does have length. Lines are used extensively in 3D modeling. A tiny formula describes an element that goes infinitely in length from one side of the environment to the other. You can think of a line as a point that has been stretched in length. A line is perfectly thin and straight. It extends infinitely in length. If you looked at a line from one end, it would look like a point. A line is infinite in length but has no width or depth as shown above. Here is my rendition of a line in space:

This is an artists rendition of a geometric line. A geometric line is referred to as 1D. That means it has length, but no width or depth.
1.4. Basic Geometric Element Three: The Plane
A plane is a slice. A plane has length and width, however, it has no depth. It is perfectly thin. A plane is a point that has been stretched in length and width but has no thickness. A plane is like a sheet of paper that is razor-thin. It has no thickness, only length and width. It is perfectly flat. A plane extends forever in length and width. If you looked at a plane from the side, it would look like a line. Think of a plane as having no thickness, but unlimited in length and width as shown above. Here is my rendition of a plane in space:

This image is an artists rendition of a geometric planel. A geometric plane is referred to as 2D. That means it has length and width, but no thickness (depth).
1.5.Basic Geometric Element Four: Space
Space is the opposite of a point. A point is infinitely small, with no length, width, or depth. Space is the opposite. Space has unlimited length, width, and depth. Think of space as taking a sphere and expanding it in all directions, infinitely, until it encompasses all of space. You can imagine space by standing outside on a night looking up at the stars. Imagine space as stretching infinitely in all directions. Space has unlimited length, width, and depth. Here is my rendition of space:
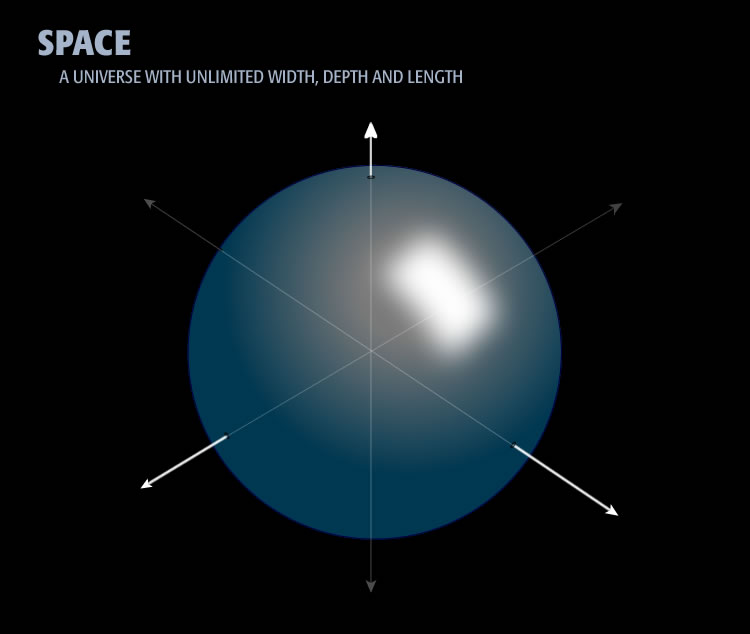
This is an artists rendition of geometric space. Here it is shown as a sphere. Space is referred to as 3D. That means it has length, width, and depth.
These four geometrical elements - point, line, plane, and space - are all that are required to prove the afterlife. We only need to look at three-dimensional software to see how pertinent geometry is to our perception of the world. Graphic artists are creating entire three-dimensional worlds using these four basic building blocks of geometry. Next, we're going to look at how geometry works in the field of three-dimensional modeling.
2. Using Three Dimensional Software to Help Visualize Geometry
2.1. Visual 3D Representation of Geometric Elements
Using geometry, a virtual reality headset, and three-dimensional software you can create an entire surrounding environment. When you put on a virtual reality headset, the world you experience is as real as the world outside. Geometry within three-dimensional software is the underlying engine that creates the environment. The underlying computer memory needed to create virtual reality is relatively small given the huge physical size of the environments they yield. We are now going to take the same geometric elements above and show how they look, feel, and act within three-dimensional software.
2.2. The Point: Intersection of Three Planes, Defined by Position
In this view, I have selected one corner of the box. The corner, shown as a white dot, is a single point. The software shows its adjacent edges in orange. The important thing to realize is the corner is a point. It is the intersection of three planes. It has only a position. It has no length, width, or depth. Shown in the lower, right inset is the mathematical location of that point. Notice how it has a single number for its location in X (1 meter), Y, and Z. There is no width to the point. It doesn't occupy a range of numbers. The corner point is a single location mathematically and within space.

This is a picture of a geometric point, modeled in 3D software. The point is the upper, left corner of the cube, shown in white. The point itself is 0D.
2.3. The Plane: The Cube's Top Face, Length, and Width without Thickness
Here I have selected the top of the cube, shown in orange. The top of the cube represents a plane. The plane has length and width but it does not have thickness. Think of a plane as being one point thick.

This is an image of a geometric plane, modeled in 3D software. The plane is shown as the top of the cube, shown in orange. The plane has length and width, but no thickness.
2.4. Space: It has Infinite Length, Width, and Depth
In this image we have all six faces of the cube selected. This represents space. Space has length, width, and depth. Three-dimensional software uses geometry to define objects in the environment. It is resolution-independent. That means no matter how close you get to an object, it will always display razor-sharp. Computer programs like Blender are able to use geometry to model three-dimensional space in stunning detail. The underlying data is compact yet the results are in robust detail. If you take this cube and expand it indefinitely, it will become the surrounding environment.

This is an image of 3 dimensional space, as modeled in 3D software. It is shown as the six sides of a cube, shown in orange. The cube is 3D meaning it has length, width, and depth.
2.5. Time: The Fourth Dimension has Duration
Time is often called the fourth dimension. Length, width, and depth, coupled with time, form our universe. The first three dimensions (point, line, space) exist in time. A point, existing through time, is a line. So to properly define a point within the context of time, it would be a point that exists for only one moment in time. The true definition of a point would have no length, no width, no depth, and no duration. But it exists. It is location, within time and space. This illustration shows the opposite. It shows a time indicator set to time location 30. You can slide the indicator to the left, to time location 20, it would show the previous environment 10 seconds ago. You can slide the indicator to the right, to move through time.

This is an image of 4 dimensional space-time, as modeled in 3d software. Here we have a 3 dimensional cube, shown with a timeline the shows its location in time. Time is the fourth dimension.
Space existing through time would have unlimited length, width, depth, and duration. The definition of space (within the context of time) would be a time-space continuum. Time-space has four dimensions. It has length, width, depth, and duration. In summary, the concepts of geometry we will use to prove afterlife include point, line, plane, space, and time. They form the logical framework for proving the afterlife. Afterlife will be proven by an equation. We will start that equation next.
3. Understanding Geometric Inverses Using Balance
3.1. Visualizing Inverse Relationship with a Balance Beam
One of the key points of Proof of Afterlife is that conscious awareness and memory are actually inversese of each other. To gain an understanding of the concept of inverse, this section employs a balance beam. On a balance beam, the two items are balance are related to (inverses of) each other. To bring the concept of inverse to life, we imagine what happens when we force the system to be in balance. Balance is a visual way to describe the concept of inverse. We all know what balance is. Take this illustration below. We have two cubes of equal size, on a balance beam, equidistant from the fulcrum. Looking at this we can see that the system is in balance.
If you start to move the fulcrum, under the balance beam, the system is gets thrown out of balance. In this view below, the fulcrum is moved toward the left box, away from the center.

In this diagram, we have two boxes on a balance beam. They are the same size, and the same distance to the fulcrum. Therefore, the system is in balance.
For the system to remain in balance, after the fulcrum is moved, the boxes need to change size. It is important to "feel" the balance of the two boxes on the beam. Since the boxes are the same size, and the fulcrum sits exactly halfway between each box, the system stays in balance. The question is, what happens when we move just one of the boxes further away from the fulcrum?
3.2. The Impact of Moving One Box Further Away from the Fulcrum
In this view, the fulcrum is moved to the left. If the boxes remain the same size, the system will be thrown out of balance.
For the fulcrum to move off-center, and for the system to remain in balance, the boxes must change size. Where the distance to the fulcrum is reduced, the size of the box must increase. Also, where the distance to the fulcrum is increased, the size of the box must decrease. In this view, you have a large box sitting on the side near the fulcrum, and you have a small box where the distance to the fulcrum is far away. The boxes, in a balanced system like this, are called inverses. That means that as one box gets larger, the other box gets correspondingly smaller.
The concept of inverse is important for afterlife. In this image below, it is important to see and feel how the boxes interact with each other in a balanced system. What happens to the one box, correspondingly happens in the opposite direction to the other box. If we keep moving the fulcrum, we are going to have a huge box on the left and a correspondly tiny box on the right. This concept of a system in balance, and inverse characteristics, come into play in the next section.

As we move the fulcrum toward the memory box, it gets larger. Consequently for the system to remain in balance, conscious awareness must get smaller.
3.3. How a Balance Beam Demonstrates Inverse
A balance beam is a simple yet effective tool for illustrating the concept of inverse. Its ability to maintain equilibrium relies on the distribution of weight across its two sides, making it a clear visual representation of how opposing actions counteract one another to achieve balance.
When a box is moved on one side of the beam, the system becomes unbalanced. To restore equilibrium, an equal and opposite action must be applied, such as decreasing the size of the moved box. This physical process reflects the mathematical idea of inverse operations. For example, addition can be undone by subtraction, just as placing a weight can be countered by moving it. Similarly, doubling the weight on one side of the beam can be reversed by halving it, demonstrating the inverse relationship between multiplication and division.
In essence, the balance beam demonstrates inverse by showing how actions have opposites that restore balance, providing a concrete foundation for understanding this fundamental concept in mathematics and beyond.
4. Demonstrating the Inverse Behavior of Boxes
4.1. We Start with Two Boxes of the Same Size
We are going to go through the inverse box analogy using Blender Three-Dimensional Software to develop a "feel" for how inverse boxes work in a balanced system. Here we have two boxes, of the same size and located at the same position in space.

In this illustration, we show two concentric cubes. The cubes are the same size, located at the same place. The control panel for each cube is shown here too.
I have put two panels in the image that show the size of each box. Both boxes are set to one.
4.2. Now Increase One Box by 20% and Decrease the other Box by 20%
Now we have taken the outer box and increased its size by 20 percent. We do this by multiplying its original size factor by 1.2 as shown on the right. Then we take the other box and make it 20 percent smaller. We do this by multiplying its original size factor by .833, as shown on the left.

In this image we have made one box slightly smaller. Then we made the other boxes correspondingly larger. You can see how the boxes were operated upon by the readings in the control panels.
The important thing to realize is that even though the size of the boxes changes, their inverse relationship holds. As one box gets larger, increasing by 20 percent, the second box gets correspondingly smaller, reducing by 20 percent. When you multiply the boxes together, 1.2 x .8333, you get one. It can be said that the two boxes are inverses of each other and the system is in balance.
4.3. Now Increase One Box by Another 20% and Decrease the other Box by Another 20%
Now we have taken the outer box and made it 20 percent larger still. We do this by multiplying its size by 1.44 as shown on the right. Then we take the inner box and reduce its size by another 20 percent. We do that by multiplying its size by .694 as shown on the left.
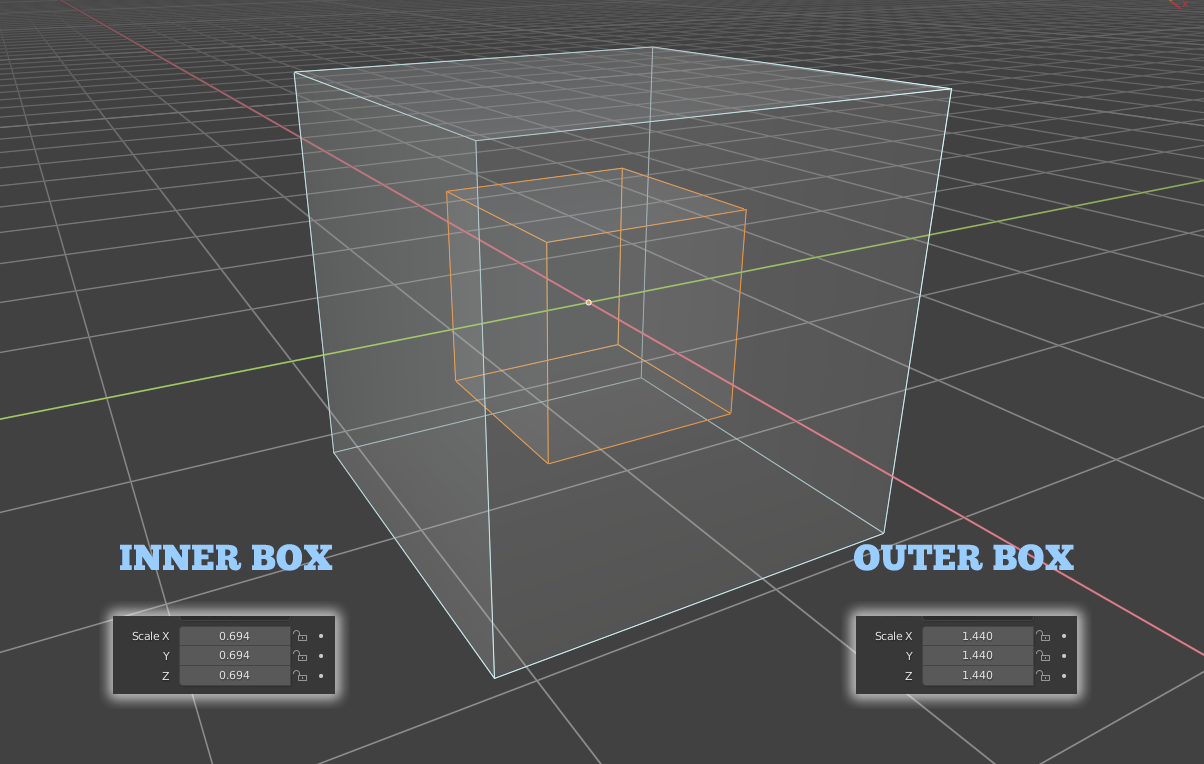
Here again we show the two concentric boxes. We have made one smaller, and the other corresponding larger, as you can see by the readings in the control panel
We are involved in driving the inner box smaller. As we do, the outer box becomes correspondingly larger. In this case, we have taken the outer box and increased it by 20 percent twice by multiplying its size factor by 1.44. Correspondly we have taken the inner box and reduced it by 20 percent twice by multiplying its size factor by .694. In every case, when the size of the two boxes is multiplied together, the answer is always one. This locks them into an inverse relationship. Whatever happens to one box has a direct opposite effect on the other box.
4.4. Now Increase One Box by another 20% Again and Decrease the other Box by another 20% Again
Now we have taken the outer box and increased it by 20 percent for a third time. We do this by multiplying its original size factor by 1.728. You can see the outer box is now so big it barely fits in the frame. That action causes the inner box and reduce its size by 20 percent for a third time. We do this by multiplying its size factor by 0.578 as shown on the left.
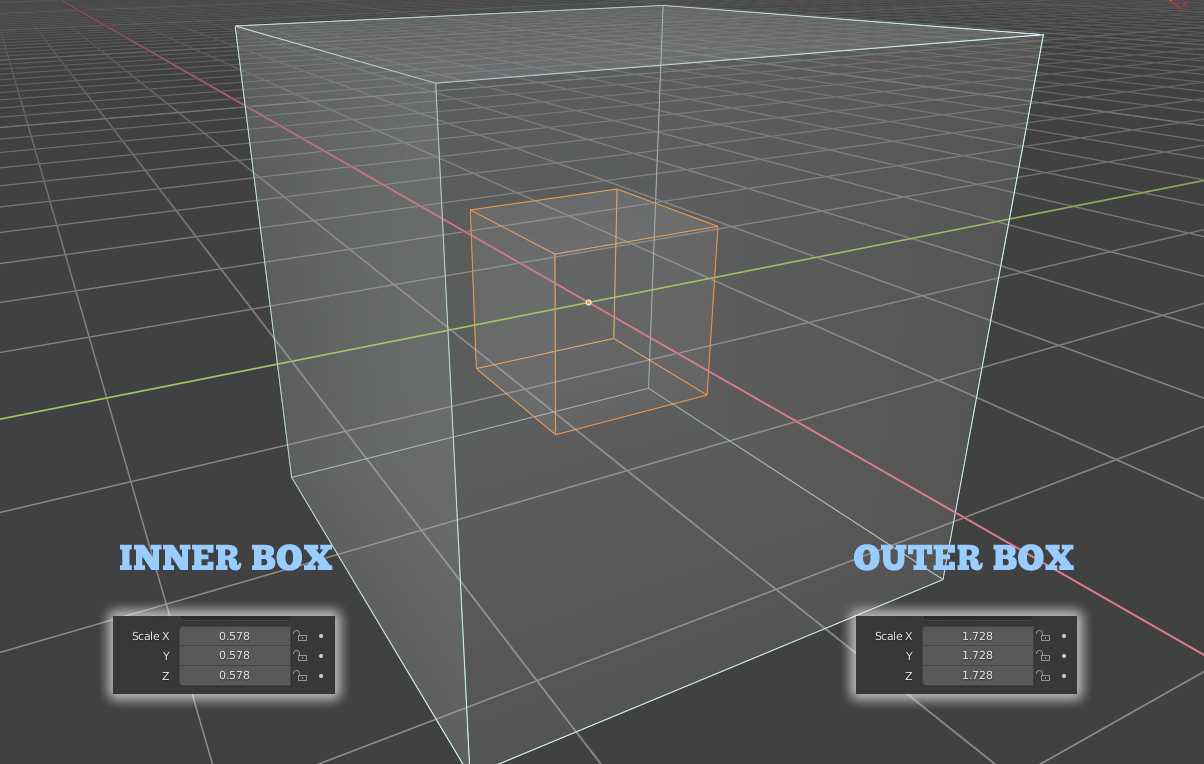
In this image, we act on the boxes once again. We make the inner box smaller. As a consequence of making it smaller, the outer box becomes correspondingly larger. Thus, the two boxes are inverses.
When you multiply the boxes together, the answer is still one, indicating their inverse relationship holds. The important thing with this exercise is to develop a "feel" for how inverse boxes act relative to each other. That feeling of how inverses work in a balanced system is an imperative concept for understanding afterlife. That concept will now be explained in the next section.
4.5. The Mathematical Elegance of Inverse Proportionality
The boxes described in the sections above demonstrate a mathematical phenomenon called inverse proportionality. Two inversely proportional boxes are those where the size of one box increases as the size of the other decreases, maintaining a constant product between the two sizes. This relationship can be mathematically expressed as:
Box1 multiplied by Box2 equals one. Here:
1. Box1 represents a dimension (such as volume) of the first box.
2. Box2 represents the corresponding dimension of the second box.
3. One is a constant that remains unchanged.
This inverse proportionality ensures that any increase in one box's size directly compensates by reducing the other, maintaining the fixed relationship defined by One.
The magic of inverse proportionality lies in its ability to maintain balance and harmony between two interdependent quantities, even as they change. In this relationship, one quantity increases precisely as the other decreases, such that their product remains constant. This principle governs a wide range of phenomena. It demonstrates how interconnected variables adapt to constraints, ensuring stability and coherence across various contexts. This elegant interplay underscores the beauty of mathematics and its role in deciphering the complexities of the world.
In the next section, we are going to take our inversely proportional magic boxes and place them on a pyramid. It is important to "feel" the inverse relationship between the boxes in the thought experiment about to ensue.
5. Afterlife Proven Mathematically Using a Pyramid
5.1. We Start with a Large, Perfect Pyramid
Imagine a pyramid - a large perfect pyramid that rises majestically from the earth with its gleaming triangular faces converging to a single, sharp apex that seems to pierce the sky. Its base, a flawless square of immense proportions, anchors the structure in geometric harmony. Its sharp edges where the faces meet trace clean, uninterrupted lines. The pyramid reflects sunlight in dazzling brilliance, casting long, sharp-edged shadows across the surrounding landscape. Its scale is both humbling and awe-inspiring. Its towering height and expansive base command attention and evoke a sense of wonder. The pyramid looks like this:

This is an artist concept of a perfect pyramid. It is infinitely large, with its base reach out to the limits of the environment. its apex as at the center of the environment.
Standing alone in an open plain, the pyramid embodies precision, symmetry, and grand scale.
5.2. Step One: Slice the Pyramid with a Plane
Now take a geometric plane (dark yellow) and make a horizontal slice through the pyramid as shown below. The horizontal slice intersects the pyramid (bright yellow) forming a plane.
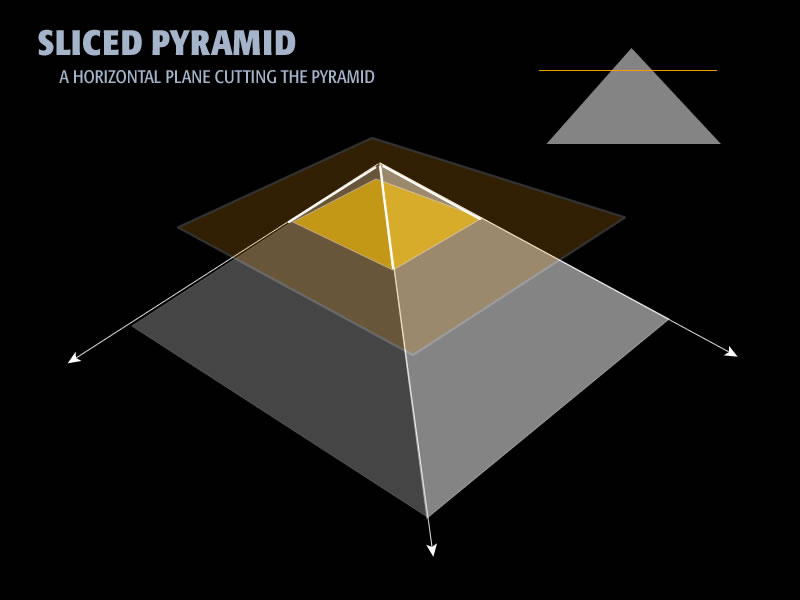
This image is an artist's rendition of a pyramid. We are above the pyramid looking down slightly. There is a yellow plane that slices the pyramid. A side view of the plane slicing the pyramid is shown on the upper right.
The small drawing in the upper right shows a side view of the plane intersecting the pyramid. The large drawing shows the plane slicing the pyramid in perspective.
5.3. Step Two: Position the Two Magic Boxes on the Slice
Now take our set of cubes and place them exactly on the slice shown in yellow. , The base of the cube sits exactly on the intersection of the slicing plane. The cube sitting on the pyramid looks like this:
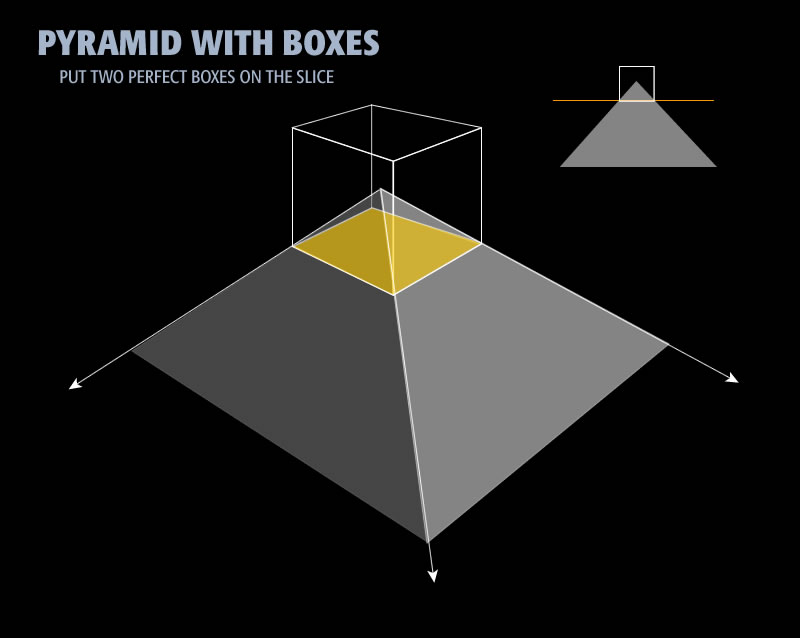
In this image, we take our two concentric boxes and place them onto the pyramid. The boxes are situated so the base of the boxes sits precisely where the plane cuts the pyramid.
The illustration in the upper right shows the set of cubes sitting on the pyramid precisely on the slice. The center of the cube sits precisely at the apex of the pyramid. The large drawing shows the cube in perspective sitting on the slice.
5.4. Step Three: Move the Plane Up Toward the Apex
The illustration below shows two boxes on the pyramid. We want to take our interesting plane and raise it slightly, up toward the apex. Notice the inset drawing at the upper right in the image above. It shows the plane has been moved up, slightly, toward the apex of the pyramid.
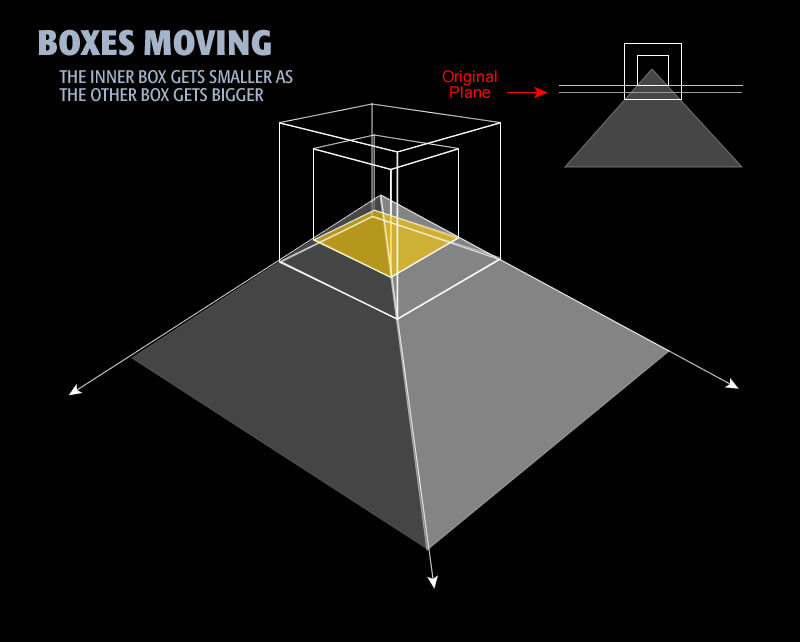
In this image, we take the slicing plane and move it up slgithly toward the apex. You can see how the plane has moved up in the small image on the upper right. As we move the plane, the base of the smaller inner box stays on the plane. This makes the inner box get smaller. As it does, the outer box get correspondingly larger. The boxes moves in inverse proportion.
This system requires that the small box stay sitting on the plane. As the plane moves up, the area of the intersection gets smaller. As a result, the inner box gets smaller too. Looking at the large image, you can see that the base of the inner box is the same size as the intersection area shown in bright yellow. The result of moving the plane up toward the apex is to force the inner box to become smaller. Its size is reduced to stay on the bright yellow intersecting area.
As we have moved the plane upward, the inner box has become smaller. Consequently, the outer box has become larger. This is because the two boxes are inverses. Being inverses, as the inner box becomes smaller, the outer box becomes correspondingly larger. In summary, we moved the slicing plane up slightly toward the apex. The inner box stayed on the plane, becoming slightly smaller. The outer box, which is the inverse of the inner box, became correspondingly larger. The system remained in balance throughout.
5.5. Step Five: Continue Elevating the Plane Towards the Apex
Now that we take the slicing plane and move it up a little further toward the apex of the pyramid. As the slice moves toward the apex of the pyramid, it takes the inner box with it. The inner box is reduced as the intersection of the pyramid is smaller. Correspondingly the outer box gets larger. As the slice moves towards the apex, the inner box becomes smaller and the outer box becomes correspondingly larger. That looks like this:
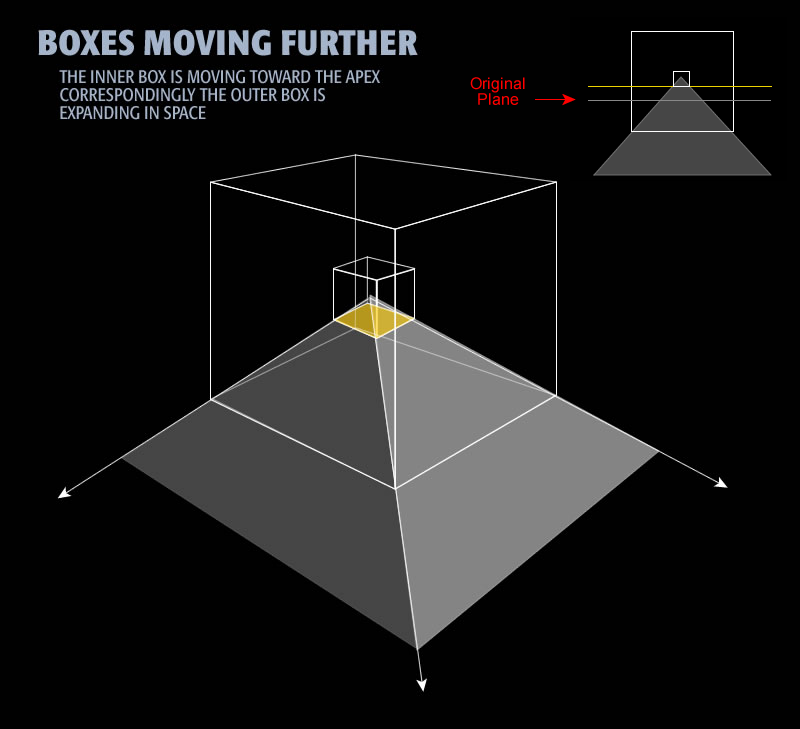
In this view, we move the plane up, toward the apex. You can see this in the side view image on the upper right. As we move the plane up, the inner box gets smaller. As the inner box gets smaller, the outer box gets correspondingly larger.
Instead of visualizing the plane and boxes moving in jumps, I want to think about constant movement. Take the slicing plane and start moving it slowly, inexorably toward the apex of the pyramid. As you move it, imagine what happens to the inner box. As you move the slicing plane up toward the apex, the inner box becomes smaller. Correspondingly the outer box is becoming larger. As you get close to the apex the inner box becomes very small. Simultaneously, its inverse, the outer box becomes very large.
5.6. Step Six: Move the Plane Up Until it Reaches the Apex
Eventually the slicing plane will reach the apex as shown below. When the slicing plane finally reaches the apex, the intersecting place, and hence the inner box, becomes a single point. It is so small that it has no length, no width, and no height but it does have position. That looks like this:
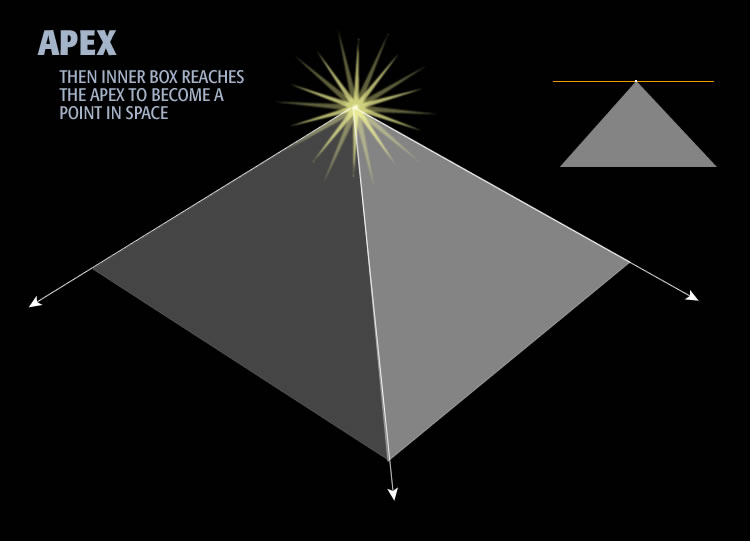
As we continue to move the plane up, eventually it will reach the apex. We it does reach the apex, it has now become so small it is a single point. Correspondly, the larger box has continued to get larger. When the inner box beomes a (0D) point, the outer box becomes (3D) space. The two boxes, one point, one space, are inverse.
The inset in the upper right shows that the slicing plane has reached the apex of the pyramid. The pyramid has perfectly sharp edges made from four geometric planes. The intersection of the slicing plane and the pyramid apex is one geometric point. The single-point inner box is sitting precisely at the apex of the pyramid. To help visualize what a single point at the apex of the pyramid looks like, imagine an infinitely small point of light. Mentally it is as if the inner cube has started to emanate light now. It has no size. It has been reduced to only position only, without dimension. Visually a close-up of the single point, formally the inner box, sitting at the apex feels something like this:

This image is an artists rendition of the moment the place reaches the apex of the pyramid. To signify the inner box becoming a point, the artist shows it glowing light. To conceptualize the moment, we have to consider its inverse, which is the entire surrounding space.
Now that the inner box has become a single point, the question is what has happened to the outer box? We will address the outer box next.
5.7. Step Seven: What Happened to the Inverse Outer Box?
We know the outer box is the inverse of the inner box. We know the inner box is a point. When the inner box became a point it had no length, width, or depth. It was infinitely small. Inversely, the outer box became infinitely large. When the inner box reached the apex, becoming a point, the outer box became the environment with unlimited length, width, and depth.
Think of the outer box expanding throughout the environment. When the inner box reached the apex, the outer cube reached out to encompass the environment. As the inner box takes on its glow when it reaches the apex, the outer box reaches out to absorb the environment entirely taking on the same glow.
In conclusion, we know three things:
1. The inner box is infinitely small, position only, with no length, width, or depth.
2. The outer box is infinitely large, with unlimited length, width, and depth.
3. The inner box and outer box are inverses of each other.
This is an artist's rendition of the view from the perspective of the outer box, looking down at the inner box:

This is the smail model shown in image 18, however here it is shown from the point of view of the outer box. This is what the outer box sees. It shows a pyramid, far away and down below, with its single point apex shining. In this model, the (0D) point apex represents conscious awareness, and the (3D) outer space represents memory.
5.8. Conclusion: What Do the Inner and Outer Boxes Represent Exactly?
Looking the the illustration above, you are sitting out in space looking at the apex of the pyramid far down below. The inner box, now a tiny point, sitting at the apex of the pyramid, is your conscious awareness. The outer space, now a large space of your surrounding environment, is your memory. So this is what we know now:
1. The inner box is infinitely small, position only, with no length, width, or depth. This is your conscious awareness.
2. The outer box is infinitely large, with unlimited length, width, and depth. This is your memory.
3. The inner box and outer box are inverses of each other. Exactly like the boxes, conscious awareness and memory are inverses of each other.
The system remains in balance.
6. Conclusion: How the Memory/Awareness Pyramid Proves Afterlife
6.1. The Dual Nature of the Human Mind
Having been through the pyramid thought experiment above, we now know that the mind is a duality, made up and both awareness [Postulate 3] and memory [Postulate 2]. The illustration below shows the dual nature of the human mind. On the left, the mind is the tiny white dot at the apex of the pyramid. That is our point of view during life. We liken this to awareness.
Conversely, as the inner box became smaller, the outer box became correspondingly larger. When the inner box reached the apex, the outer box reached out to absorb the entirety of the surrounding space. We liken that to memory.
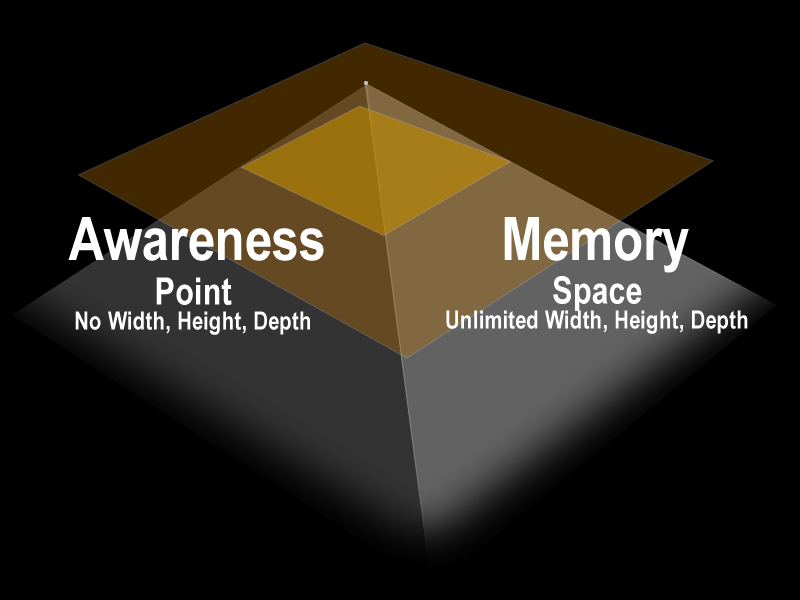
This is the same mathematical, geometric model expressed as an equation. On the left, we have the inner box. Its size has been reduced to a (0D) point, with no width, height, or depth. This is conscious awareness. On the right is the outer box. It has expanded to (3D) surrounding space, with unlimited width, height, and depth. This is memory.
In the illustration above, we set up an equation between the two aspects of the human mind as follows:
1. On the left side is awareness - position with no width, height, or depth.
2. On the right side is memory - space with unlimited length, width, and depth.
3. Awareness and Memory are inverses of each other.
This dual nature of the mind is with us always, even though we never see it. During life, we see the awareness side of the equation, position only at the center of the environment. We never see memory. Memory happens in the background. Although unseen, the implications for memory as our surrounding space are profound. It means that should awareness cease to exist, we become memory. Hence, the mind transitions from point to space. It does this by transitioning from awareness to memory. At the end of life, the mind undergoes a change in dimension from point to space. This happens in an instant, at the last moment of life.
6.2. The Mind as Space with Respect to Time
The awareness/memory equation, shown above in section 6.1, is three-dimensional only. It does not include time. To fully understand the equation and its implications for afterlife, we have to consider what happens with respect to time. In our limited three-dimensional equation, we had a point on one side and space on the other side. Now we are going to add the dimension of time to the equation as shown below.
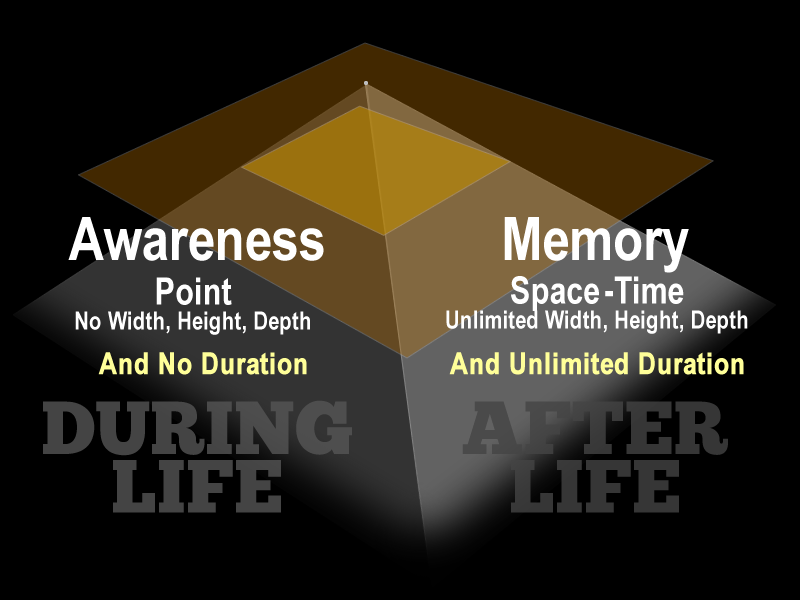
This is an equation, expressing the same geometric model. Only this time we introduce the dimension of time. On the right, we have a point, with no duration. The repesents conscioius awareness durigh life where awareness always dwells in the present. The right side is (4D) space-time. This is memory, which is the accumulation of life's experiences. The right side represent afterlife.
This is our new four-dimensional equation. It reads as follows:
1. On the left side, we have awareness - position with no width, height, depth, and no duration.
2. On the right side we have memory - space with unlimited length, width, depth , and unlimited duration.
During life, awareness can only be in one moment at a time. Awareness resides in the present moment always. The conditions for the equation above, left side, are met. Awareness is located at a unique position in space and time.
Conversely, the right side of the equation is memory. Memory extends into the past, although we don't see that. Certainly, we remember a few things in the past but that is not what we are talking about. The theory predicts that memory is total and complete and includes each moment of life. Memory doesn't just absorb what we are aware of. It absorbs everything, whether we are aware of it or not. Memory extends back in time, with each past moment being as clear, complete, and real as the present moment. We don't see this during life. However, that does not mean those memories do not exist. Each moment of life exists. It was absorbed and retained at the time it happened. Without being aware of it, during life we are developing an unlimited realm of time and space throughout a lifetime. [Postulate 4]
Do not confuse memory with remembering:
1. Remembering refers to the limited ability to call information from the past to the present.
2. Memory refers to the absorption of space of all moments that occur during a lifetime.
Remembering and memory are completely different. The consensus opinion is human memory is incomplete because people misinterpret remembering as memory. It is not. Human memory is perfect. It has absorbed all moments entirely and retained them perfectly forever.
Further understand that the "unlimited nature" of memory is relative to the individual. The right side of our four-dimensional equation predicts that memory is unlimited time and space. Unlimited space is defined as the space surrounding the individual. What happens in a galaxy across the universe is of no concern. We want to view space relative to what the individual sees. Unlimited space, relative to the individual, is the surrounding environment and everything contained within it. The implications for afterlife using this new four-dimensional model are profound. The inverse of awareness is memory. Memory includes all space and time. The inverse of awareness in a four-dimensional system is an eternity - time without beginning or end. That is how the equation balances.
At the end of life, using our four-dimensional model, life transitions from a moment in time to all time. This answers the age-old question, how can life exist after death? The answer is life does not exist after death. Life stops at the moment of death. However, the last moment of life contains all time. Inside that single point of awareness (position with time and space) is all time and space. Afterlife doesn't need to exist after a single point in time. That is because within that single point in time is all space and time. Memory make is so.
6.3. Memory: The Mind's Unseen Other Dimension
Memory, with its expanse of time and space, remains unseen during life. It takes a theory, like the one above, to predict its existence. Roughly five percent of the population have seen their memory as space. Those are people who have had an Out of out-of-body experience (OBE). During OBE, they find themselves outside their physical body, looking down at it from up above. We address OBE and its implications for afterlife in section 6.5 below.
We go through life from environment to environment. Unbeknownst to us, memory is absorbing these environments completely as we move through time. We aren't aware of it. It happens in the background. While we go about our daily lives, the mind's unseen dimension is building a realm of unlimited length, width, depth, and duration. We don't pay any attention to it. We don't even know it is happening.
Over time we accumulate a huge realm of time and space. The realm is filled with everything you have ever experienced, space, thoughts, emotions, people, etc. Memory is an unlimited realm of time and space that we have built during our lifetime. It contains everything, whether we were aware of it at the time it happened or not. We have not realized this vast realm yet. But rest assured, it is there. It has always been there. It will always be there. At the last moment of life is when this unrealized realm is realized.
6.4. Accumulated Memory: A Realm Containing Everything
At the end of life, we become unlimited space without beginning or ending. We go from a point in time to all of space and time. When I envision it, I think about the Big Bang theory of the origin of the universe. I think about how all space-time began from a single point in space-time. That is how afterlife works.
Afterlife is not a point of view within a realm. Afterlife is not awareness, being a point like we are now, but continuing beyond death. That is not how it is. Afterlife is that point of awareness changing dimension to become unlimited space. Moreover, nothing external needs to happen for this to take place. Memory as a realm is already there. The ability of awareness to expand exists too. You can think of awareness as being confined to a point during life. Once that confinement is removed, awareness expands without bounds. Awareness expansion is unlimited. It goes everywhere throughout space and time. [Postulate 8]
6.5. If You Want to See Physical Evidence, Look at Out of Body Experience (OBE)
An out-of-body experience (OBE) is a known phenomenon where your consciousness leaves your body. It happens when people get near death, such as a cardiac arrest or brain injury. People have reported experiencing OBE for centuries. It is estimated that as many as five percent of the population has experienced an OBE. That is 400 million people. Common knowledge says that your consciousness leaving your physical body is not scientifically possible. That is, until now. Now that you've been through "Proof of Afterlife by Geometry" and learned about the memory/awareness duality of life, you know what it looks like to be out in memory looking down at awareness.
99.999999 percent of the time we experience the world as consciousness looking out at memory. It is our point of view. We sit at the apex of the pyramid looking out at the world. However, for some individuals that undergo severe trauma, there is that 0.000001 of the time when this orientation flips, and find yourself looking down at your body from the outside. This flipped orientation only lasts a few seconds. Then orientation reverts to normal where consciousness looks out at memory. OBE is possible because memory is your surrounding space. For that reason, your conscious point of view can exist outside your body. Because memory is space, your point of view can be out in space, you are still within your mind. That is why OBE can and does occur.
People who have experienced true OBE are enlightened. They are enlightened because they have seen first-hand that the mind is space. They have seen what it looks like in Section 5.7 where they are out in space looking down at their body. Before OBE, they thought life at the center looking out at the world was all there is. Now they know that life in the center is just a tiny piece of the total picture. People who have seen OBE have a permanently altered attitude because they know that the mind as space exists. Once you know the mind as space exists, you know that afterlife exists. Hopefully, you know that now too, and didn't have to go through OBE to see it.
-- This concludes Proof Of Afterlife by Geometry --